[latexpage]
In this first blog post focused on marketing attribution & measurement, we share insights on how Wayfair has leveraged a unique combination of geographic splitting and optimization techniques to measure the performance of our various marketing channels
Key article takeaways:
- Geographic splitting is a convenient and generally applicable tool to create test & control groups for measuring marketing performance
- We found that naïve randomization and more complicated optimization-based techniques were not sufficient to guarantee high quality treatment & control splits
- We improved on existing optimization-based techniques by (1) incorporating more than one KPI & (2) selection of the set of treatment & control geos directly into the optimization process
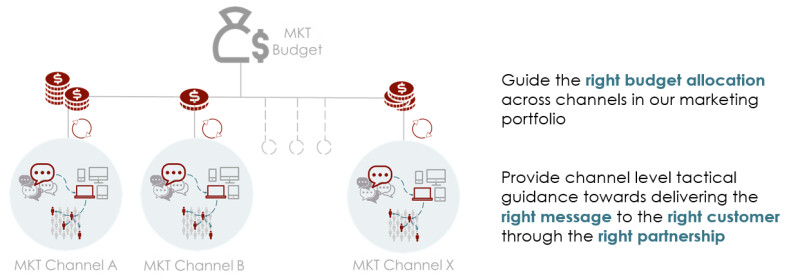
As one of the fastest growing e-commerce retailers, efficient investment across marketing channels is key to Wayfair’s success. We spent over \$400M in 2016 in marketing across our different channels, brands & geographies. These efforts are supported by dedicated teams of marketing managers & analysts, engineers and data scientists who work on marketing strategy, day-to-day adjustments and building ad tech to support marketing decision making.
Revenue lift studies are a significant part of our efforts. Precise and standardized measurement across all marketing channels enables us to discover valuable business insights that benefit all levels of decision-making (see diagram below). A prerequisite for any lift study is having treatment and control groups that behave very similarly prior to treatment. Revenue lift studies present unique challenges because treatment and control groups consist of potential customers who may have never heard about Wayfair, which complicates defining the treatment and control groups. A systematic selection of these groups while ensuring ‘alikeness’ between them over time on a set of KPIs (Key Performance Indicators) is a very challenging task.
Concept of Revenue Lift Study
At Wayfair, we assess the performance of our marketing channels through the lens of incremental revenue driven by the channel, as well as how much we spent on the marketing. Incremental revenue is how much revenue came in during certain time frame that wouldn’t have come in the absence of our marketing treatment.
Quantifying the incremental revenue (IR) is very difficult because we want to understand the causal impact of marketing. Revenue lift studies give a direct way of measuring this. The overall flow of a standard revenue lift study is described in the diagram below:
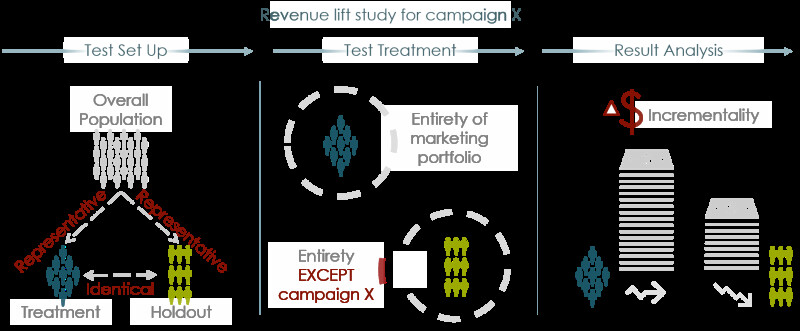
Though the concept itself is similar to an A/B test, ensuring that the selected groups are like each other across a set of target KPIs across time while still meeting a ‘strict’ sample size constraint is a very challenging task. Additionally, unlike site testing, marketing revenue lift studies may impact users who have never visited Wayfair before. As a result, in many cases, we don’t necessarily know if these users were exposed to the marketing treatment or not.
In general, the two elements to design a revenue lift study that we will explore below are:
- Choosing a test methodology suitable for nature of the specific marketing channel
- Building identical & representative treatment and control group
To address the challenges, we leverage geographic splitting and optimization.
Choosing a Suitable Test Methodology
Traffic Split vs. Geographic Split
The large set of methodologies to conduct lift studies could be classified into two main categories: Traffic split and geographic split.
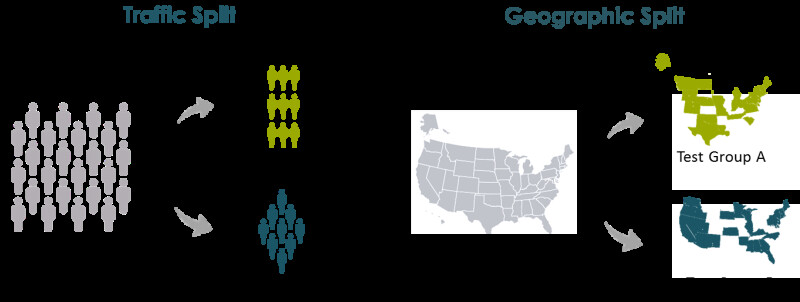
Methodologies within the traffic split category are the most commonly used, as they are simple to apply and straightforward to interpret. The traffic split can occur at different stages of the customer journey, e.g. after a site visit or even at the auction level when the lift study is run by a service provider that manages an online auction platform.
However, this method has inherent limitations for testing channels without a digital fingerprint, e.g. TV, Subway Advertisement, or Billboards. Even for online based channels like Display or Search, the ability to split at a specific stage in the customer journey is limited and generally not under the control of the advertiser. This hinders the possibilities of the advertiser to draw actionable insights from the test and also severely limits the ability to leverage traffic splitting to test online channels that target customers who haven’t recently visited our site or who are being introduced to our brand for the first time.
As a result, traffic splitting does not offer a unified methodology to test the impact of Wayfair’s full marketing portfolio.
At Wayfair, when we to validate the incremental impact a specific marketing program, we leverage a “geographic test” (often referred to as a geo-lift-study). We have successfully run geo-lift studies across a sizable portion of our marketing portfolio as:
- Most marketing platforms and partners have the ability to do geo-level targeting
- We can identify visitors in the test groups by leveraging readily available geo tracking information like IP Address
For our geo-lift studies, we use DMAs (Designated Marketing Area) as our smallest test units. DMAs offer unique advantages for ensuring test quality because their size and metropolitan-area centric design help to mitigate well known tracking accuracy issues, particularly for mobile devices.
Generating Identical & Representative Test Groups
Randomization Does Not Guarantee ‘Alike’ & ‘Representative’ Group Splits
When you have millions of test units, you can easily achieve identical performance metrics between two groups using random splitting. If the metrics are identical, we can claim that those groups are ‘alike’ and ‘representative’. However, when the maximum number of test units is instead a limited number of DMAs, randomization does not guarantee alignment between the two groups. In fact, it generally fails. See an illustrative example below:
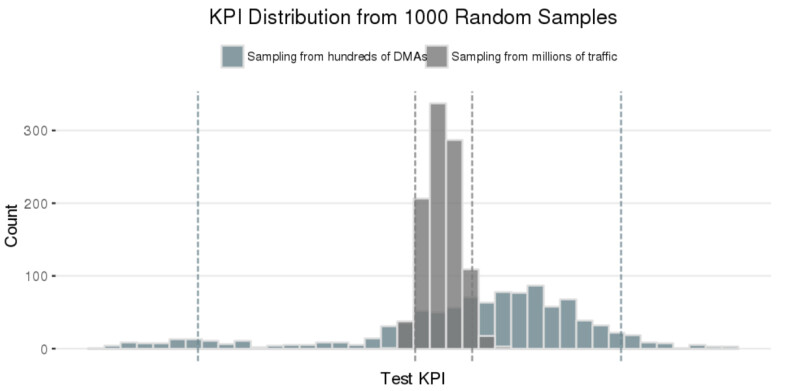
Figure 1: In the above, we generate distributions of a customer KPI by (i) taking 1000 random samples from 10% of DMAs and (ii) taking 1000 random samples from 10% of overall site traffic. The KPI distribution is much wider for (i) because the limited number of DMAs introduces bias
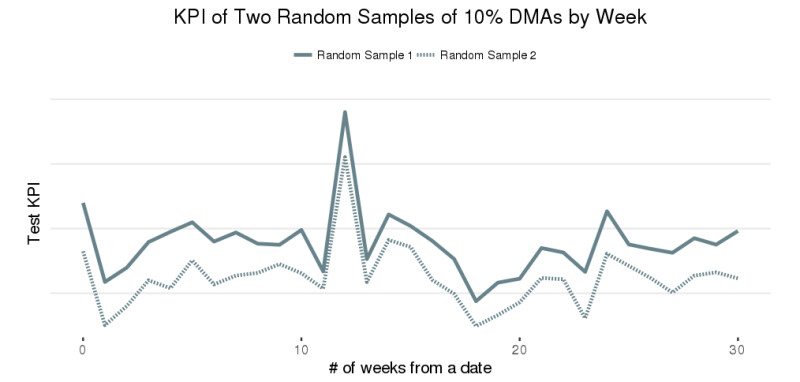
Figure 2: Time series comparing the test KPI for the two distinct 10% DMA samples. Performance is not well-aligned over time due to the small number of DMAs and the bias this introduces
As expected, with a limited number of DMAs, we cannot guarantee our two groups are ‘identical’ by randomly assigning test units to treatment/holdout group. Intuitively this makes sense if you consider the example of New York City, which is included in a single DMA. If New York City is assigned to one of your groups, we would expect it to heavily influence the performance of that group and completely change the test results! So, what else can we do to balance our group assignment at the DMA level?
Background and Definitions
Since we cannot guarantee the existence of two geos with totally ‘alike’ performance over time by randomly splitting the geo test units, we need an alternative method to isolate our treatment and holdout groups. Our method is centered on the Synthetic Control concept, frequently used to assess causality in economics and political science [1].
One can synthesize two groups to be alike as follows:
- Randomly select a subset of geos. The two groups are neither identical to each other nor representative of overall Wayfair US customer base.
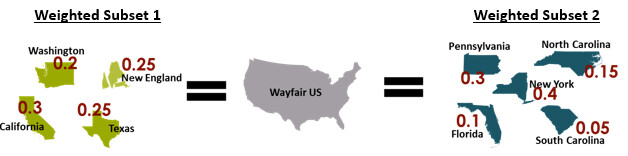
- Find weights to ‘force’ our subset of geos to mimic the whole US on our test KPI. To illustrate this concept let’s use, as an example, Washington, California, Texas and New England. Also, let’s assume that the goal of the test is to measure the impact of the treatment on revenue per visitor (RPV). We define an equation that ensures the weighted sum of the revenue per visitor for this set of synthetic geos mimics the revenue per visitor of the overall Wayfair US customer base at a given point in time:$RPV_t^{US}=\omega_{CA} \cdot RPV_t^{CA} + \omega_{WA} \cdot RPV_t^{WA} +\omega_{TX} \cdot RPV_t^{TX} +\omega_{NE} \cdot RPV_t^{NE}$Here, $RPV_t^g$ is the revenue per visitor of geo $g$ during time frame $t$ and $\omega_g$ is the weight assigned to the corresponding geo $g$. From now on, we will refer to these set of geos and their assigned weights as a synthetic test group.
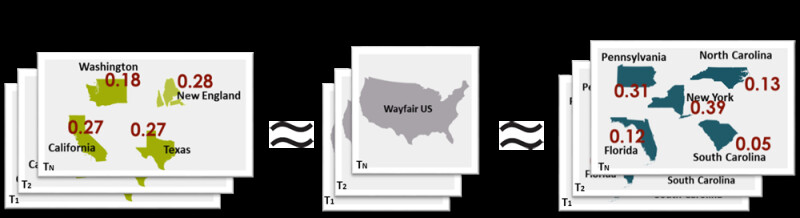
- However, we need to ensure that the matching remains consistent over time. You can always find a set of weights that make the equation valid at given time $T$. But these weights will most likely not be meaningful outside that specific point in time. Thus, the key is to synthesize two groups of geos, treatment and holdout, and ensure their similarity across time. For this purpose, someone could naively set up the problem as a large system of equations, but such a problem may have no solution. Instead, we frame it as a convex optimization problem, where the goal is to solve for a set of weights that minimize the L2 norm of the error in the synthetic representation over time:
Basic Formulation of the Optimization Problem
There are many reasonable formulations [2] of the underlying optimization problem. The optimal one will depend on the specifics of each problem. Below is a simple formulation used to find treatment and holdout set of geos whose user behaviors, through the lens of a given KPI, resemble that of average Wayfair users over time. One of the beautiful elements of such a simple formulation is that it falls within the family of convex optimization problems, which means a local minimum is also a global minimum. Thus once we find a local solution, we can be certain that we have found the best possible solution.
$$min\sum_{i=1}^{T_0}(Y_{T_{0-i}}^{US}-\sum_{j\in G} \omega_j \cdot Y_{T_{0-i}}^j)^2$$
$$s.t.\sum_{i\in G}\omega_i = 1$$
$$\omega_i \geq 0 \ \ \forall i \in G$$
Here $T_0$ denotes the start date of the test, $Y_{T_{0-i}}^j$ is the value of the target KPI in the geo unit $j$ at time $Y_{T_{0-i}}$, $\omega_i$ is the weight associated with geo $i$ in the synthetic group, and $G$ the total number of geos in the synthetic group. The optimization problem will solve for the weights $\omega_i$.
While the formulation above has nice properties, it has important limitations from the practical standpoint. It leaves the selection of candidate sets of geos to a greedy selection process, limiting its scope to selecting the optimal set of weights to minimize the discrepancies between the inputted treatment/control groups on a single KPI over time.
Improved Adaptive Optimization Problem
Our key methodological developments to adapt synthetic control method to our lift-studies were:
- Incorporating the selection of the set of geos (treatment/control) as part of the optimization problem. This at the expense of ‘falling outside’ the family of convex optimization problems
- Expanding the scope of the test to more than one test KPI, by adding the corresponding error functions to the objective function
Next, we illustrate how we modified the basic formulation to do the actual selection of the subset of geos in treatment/holdout within the optimization problem.
$$min\sum_{i=1}^{T_0}(Y_{T_{0-i}}^{US}-\sum_{j\in G} \omega_j \cdot Y_{T_{0-i}}^j)^2 $$
$$s.t.\sum_{i\in G}\omega_i = 1\ \ \ \ (1) $$
$$ \sum_{i \in G}Traffic_i \cdot x_i \leqslant Traffic_{UB} \ \ \ \ (2)$$
$$ \sum_{i \in G}Traffic_i \cdot x_i \geqslant Traffic_{LB} \ \ \ \ (3)$$
$$\omega_i \leqslant x_i\ \ \ \ (4)$$
$$x_i \in \{0,1\} \ \ \ \ (5)$$
$$\omega_i \geq 0 \ \ \forall i \in G\ \ \ \ (6)$$
We leverage the same notation as the basic formulation. Intuitively, the additional constraints control for the amount of traffic to be used in the test and the relation between weights and the decision of selecting or not the associated geo. Specifically, constraints (2) and (3) enforce that the selected geos total traffic lie within the boundaries defined by the test power analysis, constraint and (4) ensures that no weight takes non-zero value if the associated geo is not included in the grouping. Constraint (5) requires each geo to be assigned as either in or out of the grouping and finally constraint (6) ensure that all weights are non-negative.
To ‘solve’ this problem, we relax the binary constraints and leverage convex optimization algorithms to solve this ‘relaxed’ version of the problem. Now optimality is no longer guaranteed; however, but we are willing to make this tradeoff due to the nature of the problem and our ability to test the success of our matching in our data.
To validate the selection of the treatment and control groups, we divide historical data for each geo into test and training sets in time. In other words, we don’t solve the optimization problem with the entire history, but instead we leave out a subset out, to test the similarity of the resulting treatment and control groups across time. See an example below that illustrates the strong matching we can achieve in KPI performance outside the training period.
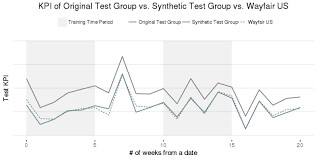
Figure 3: Compare the test KPI over time among original test group, synthetic test group and Wayfair US. Note that after applying the optimization model on the original test group over the training time (shaded area), the synthetic test group mimics Wayfair US across the time
Wrapping up…
To summarize:
- Synthetic Control Selection is used to generate two geo test groups are similar and representative of our larger US customer base over time
- Geographic Split to define test groups is a unified method to run revenue lift studies across a marketing portfolio. This method can get around several limitations across various channels and provide a more comprehensive read.
- We developed a ‘relaxed’ Convex Optimization model for the context of revenue lift study specifically, as an extension of the original synthetic control problem.
Aside from being the powerful tools to measure the true incremental contribution driven by our marketing dollars, revenue lift studies are also the best way to truly validate our in-house marketing revenue attribution model. The attribution model is another far-reaching and valued product developed by data science team, which we will introduce in future posts in this series.
Acknowledgements
Special thanks to Dan Wulin, Nathan Vierling-Claassen, Dario Marrocchelli, Bradley Fay and Timothy Hyde for the meticulous editing and invaluable feedbacks on this blog.
Authors: Lingcong (Emma) Ma, Tulia Plumettaz
Reference
[1] Abadie Alberto, Alexis Diamond, and Jens Hainmueller, “Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California’s Tobacco Control Program”. Journal of the American Statistical Association 105 (490): 493–505, 2010
[2] Abadie Alberto, Alexis Diamond, and Jens Hainmueller, “Synth: An R Package for Synthetic Control Methods in Comparative Case Studies". Journal of Statistical Software, Volume 42, Issue 13, p.1-17, 2011

